欽定古今圖書集成曆象彙編曆法典
第四十七卷目錄
曆法總部彙考四十七
明七〈鄭世子朱載堉曆學新說六〉
曆法典第四十七卷
曆法總部彙考四十七
明七
鄭世子朱載堉曆學新說六
律曆融通
《黃鍾曆》法下:〈凡四篇。〉
步月離第六
月平行,十三度三十六分八十七秒半。
離周,三百六十八度三十七分六秒。
離中百八十四度,十八分五十三秒。
《離》象,九十二度九分二十六秒半。
轉周,二十七日五十五刻四十六分。
轉中,十三日七十七刻七十三分。
轉象,六日八十八刻八十六分半。
轉差,一日九十七刻五十九分九十三秒。
圖
此處缺少一幅插圖。請考慮協助將書中此處的圖片上傳到維基共享資源,以imperial encyclopaedia - astronomy and mathematical science - pic0028.png或.svg命名。
求經朔弦朢入轉
置歲定積,來加、往減十三日二刻五分,轉周為法,除 之,不盡,來,即所求往反減轉周。各加其月朔積及弦 朢策,滿轉周去之,為所求經朔弦、朢入轉大、小餘。若 徑求次朔入轉,以轉差加之。
求疾遲初末限
視入轉大小餘,在轉中已下為疾;已上減去轉中,為 遲。置律數作限,帶律差為分,以入轉大小餘乘之,得 入限大小餘。以律數乘七音為聲數,所得入限大小 餘,在聲數已下為初限;已上,則倍聲數,減去所得入 限大小餘,為末限。
求疾遲差
置立差三秒二十五忽,以所求限大餘乘之,加平差 二分八十一秒,又以限乘之,用減定差千一百一十 一分,餘再以限乘之,滿萬為度,不滿,退除為分秒。如 是求次限積度,相減,餘為疾遲分。以乘所得初末限 下小餘,萬約為分,加入其限積度,為疾遲差。
求疾遲限下行度
置平行度及分秒,以轉象乘之,如聲數而一,所得為
一限平行度。不滿,退除為分秒。以其限疾遲分,疾初 遲末益、遲初疾末損,損益一限平行度,為所入疾遲 限下行度。
求加減差
置聲數,進一位,減去律差,各以所求盈縮疾遲差乘 之,各如所入疾遲限下行度而一,為分,不滿,退除為 秒。盈遲名為加差,縮疾名為減差。
求定朔弦朢
置經朔弦朢大小餘,各以其加減差加減之,滿或不 足,進退大餘,即定朔弦朢。視前後定朔,兩干同者,前 月大盡;不同者,前月小盡。無中氣者,為閏月。若定弦 朢小餘在日出分已下者,退一日。
求定朔弦朢加時及每日夜半晨昏入轉。
置《經朔》弦朢入轉大小餘,以定朔弦朢加減差加減 之,為定朔弦朢加時入轉;以定朔弦朢小餘減之,為 定朔弦朢晨前夜半入轉;累加一日,為每日晨前夜 半入轉;各以其日晨分加之,為晨入轉;昏分加之,為 昏入轉;滿轉周去之。
求定朔弦朢加時黃道日度。
置經朔弦朢入盈縮大小餘,以加減差加減之,為定 朔弦朢入曆。在盈便為積日,在縮加歲中為積日。命 日為度,以盈縮差盈加縮減之,為加時日行定積度; 以歲首冬至加時黃道日度加而命之,各得定朔、弦 朢加時黃道日度及分秒。
求定朔弦朢加時黃道月度。
凡定朔加時日月同度,以日行定積度即月行定積 度。弦、朢則各置其加時日行定積度,以《象策》,上弦一 加朢再加,下弦三加之,為加時月行定積度。如前加 而命之,滿躔周及黃道宿度去之,不盡,各得定朔、弦、 朢加時黃道月度及分秒。
求定朔弦朢夜半晨昏黃道月度。
置所求入轉日轉度率,與次日轉度率相減,餘以所 求入轉小餘乘之,萬約為分;前多後少減前少,後多; 加加減轉度率,為轉定度。以乘定朔弦朢小餘,萬約 為分,用減加時定積度,餘為晨前夜半定積度。以轉 定度乘其日晨昏分,萬約為分,各加夜半定積度,為 晨昏定積度;加命如前,各得夜半晨昏黃道月度及 分秒。
求每日夜半晨昏黃道月度。
累計相距日數轉度率,為轉積度,與定朔、弦、朢夜半 相距度相減;餘如相距日數而一,為日差;距度多為 加,距度少為減;加減每日轉度率,為行定度;以累加 定朔、弦、朢夜半定積度,為每日夜半定積度;累加定 朔、弦、朢晨昏定積度,為每日晨昏定積度;加命如前, 即每日夜半晨昏黃道月度及分秒。
註「曆自朔至朢,皆用昏度;既朢已後,則用晨度。」
求每日夜半晨昏赤道月度。
視所求夜半晨昏黃道月行定積度,在象策已下為 至後;滿象策去之,為分後;猶多,再去之,為至後;復多, 仍去之,為分後;以其黃道積度減之,餘以赤道率乘 之,如黃道率而一;所得,以加赤道積度及所去象策, 各為赤道定積度;以歲首冬至加時赤道日度加而 命之,滿赤道宿度去之,即每日夜半晨昏赤道月度 及分秒。
步交道第七
正交,三百六十三度七十九分三十四秒。
《中交》百八十一度,八十九分六十七秒。
距交:十四度六十六分六十六秒。
交周二十七日二十一刻二十二分二十四秒。 交中十三日六十刻六十一分十二秒。
交差,二日三十一刻八十三分六十九秒。
求經朔弦朢入交
置歲定積,來加往減,二十六日三刻八十八分,交周 為法,除之,不盡,來,即所求。往反減交周。各加其月朔 積及弦朢策,滿交周去之,為所求經朔弦、朢入交大 小餘。若徑求次朔入交,以交差加之。
求定朔弦朢加時及每日夜半入交。
置經朔弦朢入交大小餘,以定朔弦朢加減差加減 之,即定朔弦朢加時入交;以定朔弦朢小餘減之,為 定朔弦朢晨前夜半入交;累加一日,為每日晨前夜 半入交;滿交周去之。
求朔後平交入轉及加減差。
置經朔入交,與交周相減,餘為朔後平交大小餘;以 加經朔入轉,為朔後平交入轉;在轉中已下,為疾;已 上,去之,為遲。依《月離篇》求疾遲之加減差,命為正交 日加減差。
求正交日辰
置朔後平交,與經朔相併,以正交日加減、差遲加、疾 減之,為正交大小餘。滿《律總》,去之,命甲子,算外,即正 交日辰及加時小餘
求正交加時黃道月度
置朔後平交大小餘,以月平行度及分秒乘之,為距 後度;以所求月朔積命日為度,併之,為歲前冬至距 正交定積度;以冬至加時黃道日度加而命之,滿躔 周及黃道宿度去之,不盡,為正交加時黃道月度及 分秒。
求正交,在二至後初末限。
置冬至距正交定積度及分秒,在躔中已下,為冬至 後;已上,去之,為夏至後;在象策已下,為初限;已上,反 減躔中,餘為末限。
求汎差距差定限度
置初末限度,以距交乘之,如象策而一,為汎差;反減 距交,餘為距差。倍律數,以乘汎差,如距交而一,所得 交在冬至後減,夏至後加。皆加減九十八度,為定限 度及分秒。
求月離赤道正交宿度
冬至後,初限加,末限減,視春正;夏至後,初限減,末限 加,視秋正。以距差加減「春秋二正赤道宿度,為月離 赤道正交宿度及分秒。」
求正交後赤道宿積度入初、末限。
各置春秋二正赤道所當宿全度及分,以月離赤道 正交宿度及分,秋減之,餘為正交後積度。以赤道宿 度累加之,滿象策去之,為半交後;再去之,為中交後; 又去之,為半交後。視各交積度,在半象已下,為初限; 已上反減象策,餘為末限。
求每交月離白道積度及宿次。
置定限度,與初末限相減、相乘,退位為分,為定差;正 交、中交後為加,半交後為減。以差加減正交後赤道 積度,為月離白道定積度。以前宿白道定積度減之, 各得月離白道宿次及分。
《求定朔弦朢加時月離白》道宿度。
各以月離赤道正交宿度距所求定朔弦朢加時月 離赤道宿度,為正交後積度;滿象策,去之,為半交後; 再去之,為中交後;又去之,為半交後。視交後積度,在 半象已下,為初限;已上,用減象策,為末限;以初、末限 與定限度相減、相乘,退位為分,滿律母為度,為定差; 正交、中交後為加,半交後為減。以差加減月離赤道 正交後積度,為定積度;以正交宿度加之,以其所當 月離白道宿度去之,各得定朔弦、朢加時月離白道 宿度及分秒。
求每日月臨午位黃道宿度。
置月離赤道定積度,及中星所臨宿積度,上弦前後 視昏度,朢前後視夜半度,下弦前後視晨度。月在中 星已下為前,已上為後,以月星積度相減。
不及則加躔,周而復減之。
餘以其日轉定度乘之,如躔周而一,所得,前減後加 其日夜半晨昏月離黃道定積度,以歲首冬至加時 黃道日度加而命之,滿黃道宿度去之,即月臨午位 黃道宿度及分秒。
求每日月臨午位赤道宿度。
置月臨午位黃道積度及分秒,依前篇求赤道積度, 以歲首冬至加時赤道日度加而命之,滿赤道宿度 去之,即月臨午位赤道宿度及分秒。
求每日月臨午位時刻更點。
置月臨午位赤道積度及分秒,以其日晨前夜半中 星積度及分秒減之。
不及則加躔,周而後減之。
餘以律母乘之,如躔周而一,為刻,不滿,退除為分秒。 下弦已後,上弦已前,月中在晝,依時刻法求之。上弦 已後,下弦已前,月中在夜,依更點法求之。
求每日月離赤道交後初末限。
置《月離赤道正交》後積度,以赤道宿度及分累加之, 至所求月臨午位赤道宿度及分秒,在躔中已下,為 正交後;已上,去之,為中交後;在象策已下,為初限;已 上反減躔中,餘為末限。
求月離半交白道出入赤道內外度。
置各交汎差度及分秒,倍律數,加一乘之,律總加一 除之,所得視月離黃道正交在冬至後宿度為減,夏 至後宿度為加,皆加減二十三度九十分,為月離赤 道後半交白道出入赤道內外度。折半,以辰策除之, 為定差。
求月離出入赤道內外白道去極度。
置每日月離赤道交後初、末限度及分秒,用減象策, 餘為白道積;用其積度減之,餘以其差率乘之,如律 母而一,所得,以加其下積差,為每日積差。
月離白道積差差率,舊附《日躔篇》黃赤道率下。
倍辰策,以積差減之,餘以定差乘之,「為每日月離出 入赤道內外度;內減外加象策,為每日月離白道去 極度及分秒。」
求隨處月去地度及表景汎數定數。
置所求日月臨午位白道去極度及分,併其處北極出地度及分,用減躔中,餘即其處月去地度,為弧半 背。
術與日同,見《晷漏》篇。
步交食第八
日食交外限:六度。定法:六十一。
日食交內限:八度。定法:八十一。
月食限:十三度五分。定法:八十七。
求交食凡例
凡日食必在朔,月食必在朢,餘日雖交不食,視朔朢 汎交大小餘,近交周上下與交周相減,餘為距正交 分;近交中上下與交中相減,餘為距中交分。倍之,不 滿交差,為入食限。定朔加時在夜,定朢加時在晝。若 無帶食,則不必推出入,帶食則須推之。
凡定朢加時在日出後,而月食初虧於日出前者,則 退一日,只以昨夜言朢。注曆時宜預推,當退朢而不 退,是為錯誤。
求日食時差及距午分
視定朔小餘,在五十刻已下,用減五十刻,餘為中前 分;已上,減去五十刻,餘為中後分。以中前、後分與五 十刻相減、相乘,如九十六而一,為刻,不滿,退除為分 秒。中前名減,中後名加,命為時差;以併中前或中後 分,為距午分。
求《食甚入盈縮定度》。
《日食》:「置定朔加時黃道日行定積度,以時差加減之, 為食甚入盈縮定度。」月食不用時差,直以定朢加時 黃道日行定積度,便為食甚入盈縮定度,滿躔中去 之。
求日食南北差
視食甚入盈縮定度,在象策已下為初限;已上,用減 躔中,餘為末限。以初末限自相乘,千八百七十除之 為度,不滿,退除為分秒,用減四度四十六分,餘為南 北汎差。距午分乘之,半晝分除之,所得,用減汎差。〈不及〉 〈減反減之〉為「南北定差。」在縮初盈末,正交加,中交減;在盈 初縮末,正交減,中交加。
係反減者,應加卻減之,應減卻加之。
求日食東西差
置食甚入盈縮定度,與躔中相減、相乘,千八百七十 除之為度,不滿,退除為分秒,為東西汎差。距午分乘 之,二十五刻除之,為東西定差。
若在汎差已上,則倍汎差相減,餘為定差。
在縮中前,盈中後正交加,中交減。在盈中前,縮中後 正交減,中交加。
雖係倍減者,加減只如常。
求交限度
《日食》:置正交、中交度及分秒,以六度十五分為損益 差;正交損之,中交益之,以南北東西定差加減之,為 交限度。月食則不須損益加減,直以正文中交度及 分秒為交限度。
求交定度
置朔朢汎交大小餘,以月平行度乘之,以盈縮差盈 加縮減之,為交定度。若在十五度半已下,併入正交 度及分秒,為交定度。
求食差
視交定度,在正交限已下、中交限已上為交內,在正 交限已上、中交限已下為「交外」;各與限度相減,餘為 食差。
求所食分秒
各置食限,以其食差減之,餘如定法而一,為所食分 秒。不及減者,不食。食分少者,日光赫盛,或不見食。
求定限行度
置定朔朢加時入轉大小餘,依《月離》求所入疾遲限 下行度,減去八百二十分,餘為定限行度。
求定用分
日食置二十分,月食置三十分,與所食分秒相減、相 乘,平方開之,所得,日以七因,月以六因,各進二位,皆 以八百二十乘之,如定限行度而一,為定用分。
求三限時刻
《日食》:置定朔小餘,以時差加減之,為食甚分。月食不 用時差,但以定朢全分為食甚分。各以定用分減食 甚為初虧,加食甚為復圓。依時刻法求之,即三限時 刻。
求五限時刻
月食十分已上者,減去十分,餘為既;內復與十分相 減相乘,如定用分求之,為既。內分以減食甚分為食 既,以加食甚分為生光。餘同前法,共所求三限,為五 限。
求月食更點
置其日晨分,倍之,五約為更法。又五,約為點法。乃置 五限諸分,昏分已上減昏分,晨分已下加晨分。以更 法加入,如法而一,為更數。不滿,以點法加入,如法而 一,為點數
求帶食帶復
視其日日出入分,在初虧分已上,食甚分已下為帶 食,在食甚分已上,復圓分已下為帶復。各與日出入 分相減,餘名前後差,在日出入分已下為前,已上為 後。各以所食分秒乘之,如定用分而一,為日出入前 後食復分。日食:「日出已後、日入已前為見日出已前、 日入已後為不見月食,日出已前、日入已後為見日 出已後、日入已前為不見」,此與《舊法》不同。〈詳見古今交食考〉 《舊曆》無論出入,前後日月,一例求之,是屬錯誤。
求起復方所
「日食起於西,復於東,食分少者,交外偏南,交內偏北; 『月食起於東,復於西,食分少者,交外偏北,交內偏南』。」 皆指北極所在為北,日月所在為南,不必據午地論。 舊曆日月食八分已上,即言正東、正西,今惟月食十 分已上者始言之。
求食甚宿度
置食甚入盈縮定度。
日食在盈,月食在縮,無所加。日食在縮,月食在盈,加躔中。
為黃道定積度。以歲首冬至加時黃道日度加而命 之,滿黃道宿度去之,即日月食甚躔離黃道宿度及 分秒。
步五緯第九
合應。
宮土,三百六十日五千二百七十三分。
角木,二百八十日九千七十四分。
徵火,七百二十三日千七百四十五分。
商金,十二日二千六百九十六分。
羽水,四十五日八千三百二十三分。
《周率》。
宮土,三百七十八日九百一十六分。
角木,三百九十八日八千八百分。
徵火,七百七十九日九千二百九十分。
商金,五百八十三日九千二十六分。
「羽水」,百一十五日八千七百六十分。
《曆應》:
宮土,五千二百二十四日五百六十一分。
角木,千八百九十九日九千四百八十一分。
徵火,五百四十七日二千九百三十八分。
商金,十一日九千六百三十九分。
羽水,二百五日五千一百六十一分。
度率。
宮土,二十九日四千二百五十五分。
角木,十一日八千五百八十二分。
徵火,一日八千八百七分半。
商金,一日。
「羽水」一日。
伏見:
宮土十八度。
角木十三度;
「徵火」十九度。
商金,十度半。
羽水,夕伏、晨見十九度,晨伏,夕見十六度半。
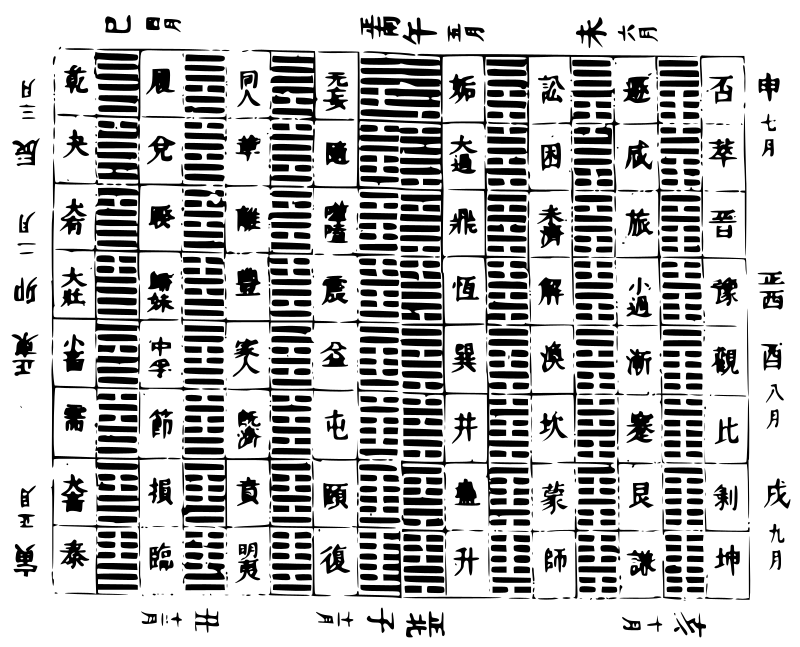
諸段積日積度
《段目》: 段日 平度 土,合伏 二十日。〈四十〉 二度。〈四十〉 晨疾: 三十一日 三度。〈四十〉 晨次疾: 二十九日 二度。〈七十五〉 晨遲: 二十六日 一度。〈五十〉 《晨留》: 三十日。
晨退: 五十二日。〈六十四五十八〉 三度。〈六十二五十四半〉 夕退 五十二日。〈六十四五十八〉 三度。〈六十二五十四半〉 夕留: 三十日。
夕遲, 二十六日 一度。〈五十〉 夕次疾: 二十九日 二度。〈七十五〉 夕疾: 三十一日 三度。〈四十〉 夕伏 二十日。〈四十〉 二度。〈四十〉 《木合伙》, 十六日。〈八十六〉 三度。〈八十六〉 晨疾,初 二十八日 六度。〈十一〉 《晨疾末》: 二十八日 五度。〈五十一〉 晨遲:初 二十八日 四度。〈三十一〉 「晨遲末」: 二十八日 一度。〈九十一〉 晨留: 二十四日。
晨退: 四十六日。〈五十八〉 四度。〈八十八十二半〉 夕退 四十六日。〈五十八〉 四度。〈八十八十二半〉 夕留: 二十四日。
夕遲:初 二十八日 一度。〈九十一〉 夕遲末, 二十八日 四度。〈三十一〉 夕疾:初 二十八日 五度。〈五十一〉 「《夕疾》末」, 二十八日 六度。〈十一〉 夕伏 十六日。〈八十六〉 三度。〈八十六〉《火合伏》, 六十九日 五十度。 《晨疾》初 五十九日 四十一度。〈八十〉 《晨疾末》: 五十七日 三十九度。〈○八〉 晨次疾初 五十三日 三十四度。〈十六〉 晨次疾末: 四十七日 二十七度。〈○四〉 晨遲:初 三十九日 十七度。〈七十二〉 「晨遲末」, 二十九日 六度。〈二十〉 晨留: 八日。
晨退: 二十八日。〈九十六四十五〉 八度。〈六十五六十七半〉 夕退 二十八日。〈九十六四十五〉 八度。〈六十五六十七半〉 夕留: 八日。
夕遲,初 二十九日 六度。〈二十〉 夕遲末, 三十九日 十七度。〈七十二〉 夕「次疾」初 四十七日 二十七度。〈○四〉 夕次疾末: 五十三日 三十四度。〈十六〉 夕疾:初 五十七日 三十九度。〈○八〉 《夕疾末》: 五十九日 四十一度。〈八十〉 夕伏 六十九日 五十度。 金合伏 三十九日 四十九度。〈五十〉 夕疾:初 五十二日 六十五度。〈五十〉 《夕疾末》, 四十九日 六十一度。 《夕次疾》初, 四十二日 五十度。〈二十五〉 夕次疾末, 三十九日 四十二度。〈五十〉 夕遲初 三十三日 二十七度。 夕遲末 十六日 四度。〈二十五〉 夕留: 五日。
夕退 十日。〈九十五十三〉 三度。〈六十九八十七〉 夕退伏 六日 四度。〈三十五〉 《合》退伏 六日 四度。〈三十五〉 晨退 十日。〈九十五十三〉 三度。〈六十九八十七〉 晨留: 五日。
晨遲:初 十六日 四度。〈二十五〉 晨遲末, 三十三日 二十七度。 《晨次疾》初, 三十九日 四十二度。〈五十〉 晨次疾末: 四十二日 五十度。〈二十五〉 《晨疾》初 四十九日 六十一度。 《晨疾》末 五十二日 六十五度。〈五十〉 晨伏 三十九日 四十九度。〈五十〉 《水合伏》, 十七日。〈七十五〉 三十四度。〈二十五〉 夕疾: 十五日 二十一度。〈三十八〉 夕遲, 十二日 十度。〈十二〉 夕留: 二日。
夕,退伏 十一日。〈十八八十〉 七度。〈八十一二十〉 「合退伏」 十一日。〈十八八十〉 七度。〈八十一二十〉 晨留: 二日。
晨遲: 十二日 十度。〈十二〉 晨疾: 十五日 二十一度。〈三十八〉 晨伏 十七日。〈七十五〉 三十四度。〈二十五〉 段目 限度, 初行率 土,合伏 一度。〈四十九〉 十二分 晨疾 二度。〈十一〉 十一分 晨次疾 一度。〈七十一〉 十分 晨遲 初。〈八十三〉 八分, 《晨留》:
晨退 初。〈二十八四十五半〉
夕退 初。〈二十八四十五半〉 《十分 夕留》:
夕遲: 初八十三。
夕,次疾 一度。〈七十一〉 八分 夕疾 二度。〈十一〉 十分 夕伏 一度。〈四十九〉 「十一分 木合伏」 二度。〈九十三〉 二十三分 「晨疾」初 四度。〈六十四〉 二十二分 《晨疾》末 四度。〈十九〉 二十一分 晨遲初 三度。〈二十八〉 十八分 晨遲末 一度。〈四十五〉 十二分 晨留:
《晨退 空》:〈三十二八十七半〉
夕退 空。〈三十二八十七半〉 十六分 夕留:
夕遲初 一度。〈四十五〉
夕遲末 三度。〈二十八〉 十二分 夕疾初 四度。〈十九〉 十八分 《夕疾》末 四度。〈六十四〉 二十一分 夕伏 二度。〈九十三〉 二十二分 《火》合伏 四十六度。〈五十〉 七十三分 晨疾初 三十八度。〈八十七〉 七十二分 《晨疾》末 三十六度。〈三十四〉 七十分 晨次疾初 三十一度。〈七十七〉 六十七分 「晨次疾」末 二十五度。〈十五〉 六十二分 晨遲初 十六度。〈四十八〉 五十三分晨遲末 五度。〈七十七〉 三十八分 《晨留》
晨退 六度。〈四十六三十二半〉
夕退 六度。〈四十六三十二半〉 四十四分, 夕留:
夕遲初 五度。〈七十七〉
夕遲末 十六度。〈四十八〉 三十八分 夕次疾初 二十五度。〈十五〉 五十三分 夕「次疾」末 三十一度。〈七十七〉 六十二分 夕疾初 三十六度。〈三十四〉 六十七分 《夕疾》末 三十八度。〈八十七〉 七十分 夕伏 四十六度。〈五十〉 七十二分 金合伏 四十七度。〈六十四〉 一度。〈二十七分半〉 夕疾初 六十三度。〈○四〉 一度。〈二十六分半〉 夕疾末, 五十八度。〈七十一〉 一度。〈二十五分半〉 夕次疾初 四十八度。〈二十六〉 一度。〈二十三分半〉 夕次疾末 四十度。〈九十〉 一度。〈十六分〉 夕遲初 二十五度。〈九十九〉 一度。〈二分〉 夕遲末 四度。〈○九〉 六十二分, 夕留:
夕退 一度。〈五十九十三〉
夕退伏 一度。〈六十三〉 六十一分 合退伏 一度。〈六十三〉 八十二分 晨退 一度〈五十九十三〉 六十一分 《晨留》:
晨遲:初 四度。〈○九〉
晨遲末 二十五度。〈九十九〉 六十二分 晨次疾初 四十度。〈九十〉 一度。〈二分〉 晨次疾末 四十八度。〈三十六〉 一度。〈十六分〉 晨疾初 五十八度。〈七十一〉 一度。〈二十三分半〉 晨疾末: 六十三度。〈○四〉 一度。〈二十五分半〉 晨伏 四十七度。〈六十四〉 一度。〈二十六分半〉 《水合伏》 二十九度。〈○八〉 二度。〈十五分五十八〉 夕疾 十八度。〈十六〉 一度。〈七十分三十四〉 夕遲 八度。〈五十九〉 一度。〈十四分七十二〉 《夕留》:
夕退伏 二度。〈十分八十〉
「合」退伏 二度。〈十分八十〉 一度。〈三分四十六〉 《晨留》:
晨遲 八度。〈五十九〉
晨疾: 十八度。〈十六〉 一度。〈十四分七十二〉 晨伏 二十九度。〈○八〉 一度。〈七十分三十四〉
求五星平合日
置歲定積,來減往加其星合應,滿其周率去之,不盡, 往即所求來。反減周率,即歲首冬至後平合日及分 秒。
求諸段積日積度
副置平合日及分秒,累加段日,即諸段積日。命日為 度,累加平度,退則減之,即諸段積度及分秒。
求諸段入曆
置歲定積,以其星《曆應》併所求平合日及分秒,來加、 往減之,如其度率而一,為度,不滿,退除為分秒。滿曆 率去之,來即所求往反。減曆率,即平合入曆度。累加 限度,各得其段入曆度及分秒。
求盈縮初末限
置各段入曆度及分秒,若在躔中已下,為盈;已上,減 去躔中,為縮。其土、木、金、水四星諸段,在象策已下,為 初限;已上,用減躔中,餘為末限。其火星諸段,盈者在 二,因辰策已下;縮者在四,因辰策已下,為初限;已上, 用減躔中,餘為末限。
求盈縮差
土星:盈者,立差二秒八十三忽,加平差四分十秒二 十二忽,減定差千五百一十四分六十一秒。縮者,立 差三秒三十一忽,加平差一分五十一秒二十六忽, 減定差千一百一分七十五秒。
《木星盈縮立差》,二秒三十六忽,加平差二分五十九 秒十二忽,減定差千八十九分七十秒。
《金星盈縮立差》,一秒四十一忽,加平差,三忽,減定差, 三百五十一分五十五秒。
水星盈縮立差一秒四十一忽,加平差二十一秒六 十五忽,減定差三百八十七分七十秒。
火星《盈初縮末立差》,十一秒三十五忽,減平差八十 三分十一,秒八十九忽,減定差八千八百四十七分 八十四秒。《縮初盈末立差》,八秒五十一忽,減平差三 分二秒三十五忽,減定差二千九百九十七分六十 三秒。
新改縮初盈末立差,一,秒二十四忽,減平差二十分三十秒,減定差四千三百九十二分。
各置立差,以所求初末限度,反分秒乘之,加減平差, 再乘之,用減定差,又乘之,滿萬為度,不滿,退除為分 秒,為盈縮差又法:置所求初末限下小餘,以其限盈縮分乘之,萬 約為分,加入其限積度,亦為盈縮差。
求諸段定積日及日辰
各置其段積日,以其盈縮差盈加縮減之,即其段定 積日及分秒。以歲首黃鍾正律大、小餘加之,滿律總 去之,其大餘命甲子算外,即得日辰及加時小餘。
求諸段所在月日
各置其段定積日及分秒,加閏餘,減朔策,餘如朔策 而一,為月數,不盡,為入經朔已來日數。其月數,命正 月若在朔策已下,不及減者,為入年前;十一月;已上, 去之,為入十二月。俱以日辰所在為定。凡閏餘在十 六日已上,則其年有閏,依求汎閏術定之。
求諸段加時定積度
各置其段積度,以其盈縮差盈加縮減之。〈金星再之水星三之〉 「即諸段加時定積度。」以歲首冬至加時黃道日度,加 而命之,即其星其段加時所在宿度及分秒。
求諸段初日晨前夜半所在宿度。
各以其段初行率,乘其段加時小餘,如律母而一,為 分,順減、退加其日加時定積度,即其段初日晨前夜 半定積度;加命如前,即得所在宿度及分秒。
求諸段日率度率及平行分。
各以其段日辰與後段日辰相距數為日率,以其段 夜半積度與後段夜半積度相減,餘為度率。各置度 率及分秒,以其日率除之,即其段平行分。
求諸段增減差及日差
以本段前後平行分相減,為其段汎差;倍而退位,為 增減差。前多後少者,加為初,減為末;前少後多者,減 為初,加為末。以加減其段平行分,為初末日行分。 又倍增減差,為總差;以日率減一除之,為日差。
求前後伏遲退段增減差。
前伏者,置後段初日行分,加其日差之半,為末日行 分。後伏者,置前段末日行分,加其日差之半,為初日 行分;以減伏段平行分,餘為增減差。
前遲者,置前段末日行分,倍其日差減之,為初日行 分;後遲者,置後段初日行分,倍其日差減之,為末日 行分;以前後近留之遲段平行分減之,餘為增減差。 土木火三星退行者,六因平行分,退一位,為增減差。 金星前後退伏者,三因平行分,半而退位,為增減差; 前退者,置後段初日行分,以其日差減之,為末日行 「分。後退」者,置前段末日行分,以其日差減之,為初日 行分;以本段平行分減之,餘為增減差。
水星退行者,半平行分,為增減差。
皆以增減差加減平行分,為初末日行分前多後少 者,加為初,減為末;前少後多者,減為初,加為末。 又倍增減差,為總差,以日率減一除之,為日差。
求每日晨前夜半星行宿度。
各置其段初日行分,以日差累損益之,後少則損之, 後多則益之,「為每日行度及分秒。乃置其段初日晨 前夜半定積度,順加退減,滿宿度去之,即每日晨前 夜半星行宿度及分秒。」
求平合見《伏入太陽盈縮曆》。
置其星其段定積日及分秒,在歲中已下,為盈;已上 去之,為縮;多則再去之,復為盈;各在初限已下,為初 限;已上反減歲中,餘為末限。即其星平合見伏入曆 日及分秒。
求平合見伏星與太陽行差。
各以其星其段初日星行分與其段初日太陽行分 相減,餘為行差。若金、水二星退行在退合者,以其段 初日星行分併其段初日太陽行分,為行差。其水星 夕伏、晨見者,直以其段初日太陽行分,為行差。
求定合定見定伏汎積日。
土、木、火三星,各以平合晨見夕伏定積日,便為定合 伏見汎積日及分秒。
《金星》:「置其段盈縮差,水星倍置之,各以其段行差除 之,為日,不滿,退除為分秒。在平合夕見、晨伏者,盈減 縮加;在退合夕伏、晨見者,盈加縮減。各加減定積日, 為定合伏見汎積日及分秒。」
求定合定積日、定積度。
「土、木、火三星,各以平合行差除其段初日太陽盈縮 積,為距合差日,不滿,退除為分秒,以太陽盈縮積減 之,為距合差度;副置其星定合汎積,以距合差日差 度盈減縮加之,為其星定合定積日定積度及分秒。」 此與下條言「盈縮」者皆指太陽,非謂本星。
金、水二星順合退合者,各以平合退合行差除其日 太陽盈縮積,為距合差日;不滿,退除為分秒;順加退 減太陽盈縮積,為距合差度。順合者,以距合差日差 度盈加縮減其星定合汎積,為其星定合定積日定 積度及分秒。退合者,以距合差日盈減縮加,以距合 差度盈加縮減加減「其星退定合汎積,為其星退定」 合定積日定積度及分秒;加命如前,各得所求日辰 及宿度分秒徑求合伏定日者,土、木、火三星以夜半黃道日度減 其星夜半黃道度,餘在其日太陽行分;已下者,金、水 二星以其星夜半黃道度減夜半黃道日度,餘在其 日本星行分已下者,各為其日合伏。係合退伏者,視 其日夜半黃道日度,未「行到本星度,及視次日太陽 行過本星度,而本星退行過太陽宿度者,為其日合 退伏。」
求定見定伏定積日
「『土、木、火三星,各置定見、定伏汎積日及分秒,以歲中 折半,晨加夕減之,在歲中已下,自相乘,已上,倍歲中, 反減之,餘亦自相乘,七十五而一,為分,不滿,退除為 秒,以其星見伏度乘之,十五除之,所得,滿行差而一 為日,不滿,退除為分秒;見加伏減汎積,為其星定見、 定伏定積日及分秒;加命如前,即得定見、定伏日辰』。 金、水二星,各以伏見日行差除其段初日太陽盈縮 積,為日,不滿,退除為分秒。夕見、晨伏,盈加縮減;晨見、 夕伏,盈減縮加。加減其星定見、定伏汎積日及分秒, 為常積。若在歲中已下,為冬至後」;已上,去之,為夏至 後。在歲中,折半已下,自相乘,已上反減歲中,餘亦自 相乘。冬至後晨,夏至後夕,十八而一,為分;冬至後夕, 夏至後晨,七十五而一為分;以其星見伏度乘之,十 五除之,所得,滿行差而一為日,不滿,退除為分秒。「晨 見、夕伏,冬至後加,夏至後減;夕見、晨伏,冬至後減,夏 至後加。皆加減常積,為其星定見、定」伏定積日及分 秒;加命如前,即得定見、定伏日辰。〈以上律曆融通係原本卷之二〉
《黃鍾曆議》上。〈凡五篇。〉
律元
《曆距》曰:「元。元者,萬物之始,眾善之長,所以統三辰之 會也。天有三辰,地有五行,太極運三辰五星於上,而 元氣轉三統五行於下;其於人皇極統三德五事。故 三辰合於三統,五星合於五行,日合於天統,月合於 地統,斗合於人統,水合於辰星,火合於熒惑,木合於 歲星,金合於太白,土合於填星,三辰五星,而相經緯」 也。夫三五相包而生,故三統合於一元。因元一而九 三之以為法,十一三之以為實,實如法而一得黃鍾 長九寸。太極中央元氣,謂之黃鍾,其長九寸者,陽氣 之全也。故黃鍾紀元氣之謂律。律者,法也,莫不取法 焉,是為萬事根本。天道運行,循環無端。術家推步,氣 朔盈虛,日月躔離,五星伏見,上考已往,下驗方來,則 必皆以曆元為距。故曆元者,所以因之起算者也。《後 漢志》曰:「黃帝造曆,元起辛卯,顓頊用乙卯,夏用丙寅, 殷用甲寅,周用丁巳,魯用庚子。」六家古曆,立元各殊, 積算遠近,今不可考。後世治曆者,或求諸遐邈,或距 諸目前,歷代諸曆,殆有百家,無一同者。《三統曆》以十 四萬年已上為元,《麟德曆》以二十六萬年已上為元, 《皇極曆》以百萬年已上為元,《大衍曆》以九千六百九 十六萬年已上為元,此皆取諸曠古者也。《太初曆》就 以太初元年丁丑歲為元,《戊寅曆》初則以武德元年 戊寅歲為元,《授時曆》以至元十八年辛巳歲為元,《大 統曆》以洪武十七年甲子歲為元,此皆取諸當時者 也。或「遠或近,雖則相縣,要之順天求合則密,為合驗 天則疏。此前人定論也。古法推步七政,多求其總,會 於甲子逆考順推,上下數千萬年,而諸曆履端歸餘, 遠近多寡,為數不同。」竊嘗論之,唐李淳風、僧一行蓋 精於曆數矣,然淳風《麟德曆》已為一行所非,而一行 《大衍曆》推今冬至,凡差二日,則其積年日法俱不可 求。曆元之始終,豈非以歲遠故難測耶?豈天地生數 之始,果如是紛糅耶?抑好奇者為之故爾?又有所謂 元會運世命為曆法者,初無其事,但以十二與三十 相參,甲子為之。夫氣朔有盈虛,故有大盡小盡,因此 以置閏,古之道也。例以三十為用,是以一定之數,推 不齊之運,猶月皆大盡,亦「不置閏也。」世儒雖惑之,而 曆家不取其說,惟所謂《截元曆》者,但以測驗真數為 則,不復逆考順推以求其齊。元大儒許衡等造《授時 曆》,實用其術,而積年日法在所不取,其見卓矣。皇朝 《大統曆》雖稍損益,多因舊法,故超勝諸曆,而行之最 久,是知衡曆可以為百世之師範也。今黃鍾算術以 萬曆九年「辛巳歲為距者,其旨有三:一者貴其名,二 者貴其義,三者貴其時。」夫貴其名何也?按《玉海》諸書 皆云:「伏羲元年辛巳,在位百二十年。神農元年亦辛 巳,在位百二十年。」說者或以為黃帝命大撓始作甲 子,然辛巳之名已見於羲農之世,其非大撓始作明 矣。六十甲子迨與天地俱生,其來尚矣,莫知誰所造 也。以為大撓始作,非也。《干支紀年》,見於史者,辛巳其 為權輿乎?夫羲農二聖,適同辛巳之元,皆躋上壽之 域,此尤可欽羨也。是故表而出之。伏願當今體無為 之化,協萬壽之徵,此所以貴其名也。貴其時義,何也? 《易》革卦之象,「君子以治曆明時,而湯武以之,所謂順 乎天而應乎人。」考諸三代而下,「創業之君,順天應人者,不無其人。若夫治曆明時,或未及為,則有待於後 王。」是故漢高祖革命之後,襲秦《正朔歷》。孝、惠、文、景三 君,至武帝太初元年方議造《漢曆》。漢興至此百餘歲 矣,後又三十餘歲,至元鳳六年,而是非堅定。唐高祖 創業之時,雖嘗治曆,而法未密。歷太高、中、睿四君,至 元宗開元九年,始命僧一行改造《大衍曆》。唐興至此, 亦百餘歲,而儀式方備。是知歷代帝王草創之初,固 有未及為者,全賴嗣君善繼善述以成其志耳。我太 祖高皇帝創帝業,奠華夏,順天應人,莫大於此。雖湯 武有所不及,而革命之際,距勝國至元辛巳歲纔八 十七年。《授時曆》積算未久,氣朔不差,故仍舊貫,無所 改作,略加潤色而已。然彼辛巳至今萬曆辛巳,三百 年矣。年遠數盈,漸差天度,古人所謂「三百年斗曆,改 憲治曆明時」之期,豈非在於斯乎?恭惟祖宗列聖御 極以來,改元建號,未嘗以曆為名。至我皇上,始以萬 曆為年號,而適當改憲之際。此乃天運潛符,為《聖壽 萬年曆》之元矣。九者陽數,大哉乾元,位尊九五,飛龍 在天之象,故以九年表之。古之人論數也,曰:「物生而 後有象,象而後有滋,滋而後有數。」夫沖漠之間,兆眹 之先,數之原也。有儀有象,判一而兩,數之分也。日月 星辰垂於上,山嶽川澤奠於下,數之著也。四時迭運 而不窮,五氣以序而流通。風雷不測,雨露之澤,萬物 形色,數之化也。聖人「繼世,經天緯地,立茲人極,稱物 平施,父子以親,君臣以義,夫婦以別,長幼以序,朋友 以信,數之教也。」「分天為九野,別地為九州,制人為九 行,九品任官,九井均田,九族睦俗,九禮辨分,九變成 樂,九刑禁姦」,九寸為律,九分造曆,九筮稽疑,九章命 算,九職任萬民,九賦斂財賄,九式節財用,九府立圜 法,九服,辨邦國九命,位邦國九儀,命邦國九法,平邦 國九伐,正邦國九貢,致邦國之用,九兩,繫邦國之民, 營國九里,制城九雉,九階九室,九經九緯,數之度也。 《律書》曰:「王者制事立法,物度軌則,壹稟於六律。」六律 為萬事根本,故取黃鍾之律,其長九寸,以表萬曆九 年為曆之元。蓋託義倚數,用為推步之距而已。或云: 漢雒下閎倚數起於黃鍾之龠,其法一本於律。至唐 一行,乃始專用大衍之策,則曆術又本於《易》。是皆傅 會之說,何必踵其故習哉?不然,蓋曆起於數,數者,自 然之用也,其用無窮而無所不通,以之於律、於《易》,皆 可以合也,要在順天求合而已。且夫取象之說,於經 有之,歸奇象閏,再閏象扐之類,初非揲卦本旨,特取 象之說耳。以為涉於傅會,不亦過歟?或云:若以萬曆 元年為距,何如?曰:「《易》不云乎:『大衍之數五十,其用四 十有九。一元太極,妙不可言,能以美利利天下,而不 言所利,是故乾元惟用九耳。故曰:『顯諸仁,藏諸用』。《春 秋傳》曰:『元年者,人君之用也。大哉乾元,萬物資始。天 之用也。至哉坤元』』」,「萬物資生」,地之用也。成位乎其中, 則與天地參。故體元者人君之事,而調元者,宰相之 職。然推步之家用以為距者,特取斗曆改憲一節而 已。蓋辛巳歲適當其際,故用為距,而以曆元命之,亦 猶《大統曆》不以洪武元年為元,而以甲子歲為元也。
律母
「道生於一,謂之太一。」太一者,太極也。由一生二,是為 兩儀;由二生三,是為三才;由三生四,是為四象;由四 生五,是為五行。總而言之,凡數皆生於一。一者,五行 之本,萬物之元也。是故二者一之與一也;三者一之 與二也;四者一之與三也;五者一之與四也。其上之 一,數之母也;其下之一二三四,數之子也。去母言之, 惟有一、二、三四而無五;加母言之,則有二、三、四、五而 無一。一者先天也,五者後天也。後天不見其所生,先 天不見其所成,蓋自然之理也。由五已往,則一為之 本;由五已來,則五為之元。是故六者五之與一也,七 者五之與二也,八者五之與三也,九者五之與四也, 十者五之與五也。此謂一為五數之本,五為萬數之 元也。《傳》曰:「天地與我並生,萬物與我為一。一與一為 二,二與一為三。」自此以往,巧歷不能得,而況其凡乎? 推其本元而論之,不過一二三四而已。《傳》曰:「古之所 謂道術者,無乎不在其數,則一二三四是也。」此之謂 歟。數術之要妙,在乎七之與九,何也?夫道化而為一, 一者太一也,物之祖「也,數之根也。一化而為七,其象 則圓。七化而為九,其象則方。」九者,究也,乃復化而為 一,則歸於其根矣。夫「七生於《坤》,《坎》,與六為表裏,故其 體圓而用方。九生於《乾》,《離》,與八為表裏,故其體方而 用圓。是故七中減一者。」�六也。☷《坤》之象也。六中加 一者。�七也。☷「坎」之象也。《坤》之與「坎」,皆根於陰者也, 九中減一者,�八也。☲《離》之象也。八中加「一」者。�九 也。☰乾之象也。乾之與離,皆根於陽者也。故《洛書》之 位九居於上,《河圖》之位六居於下,而乾坤定矣;《洛書》 之位七居於右,《河圖》之位八居於左,而坎離交矣。《河 圖》《洛書》相為經緯;八卦九疇,相為表裏;故九為老陽, 而六為老陰,七為少陽,而八為少陰。《易》之為書,至理 要道,不過七八九六數言而已。一二三四者,六七八九之「所以生;六七八九者,一二三四之所以成。」十者, 一之全數也,五者,十之半數也。是故十半之則為五, 五倍之而為十,十即一也,百千萬億亦猶一也,乃至 溝澗正載,不可說數,亦不過乎一也。此算術之至妙 者歟!《易》曰:「天一地二,天三地四,天五地六,天七地八, 天九地十。奇數究於九,偶數甚於十。十者,天地之全 體,九者天地之大用,此所以成變化而行鬼神也。」何 瑭氏曰:「造化之道,一陰一陽而已矣。陽動陰靜,陽明 陰晦。陽無體以陰為體;陰無用待陽而用。二者相合 則生,相離則滅。微哉微哉!通於其說,則鬼神之幽,人 物之著,天文地理,一以貫之而無遺矣。九為陽精,主 於施;十為陰精,主於化。施」者,萬物之父,化者,萬物之 母。故九寸為律元,十寸為度母。算律之率,以九為黃 鍾之經分,以十為黃鍾之約分。就經分而言,故曰「黃 鍾之律,其長九寸。」就約分而言,故曰「黃鍾之度,其長 十寸。」九寸、十寸,名異實同,而先儒未達也。何氏曰:「《漢 志》謂黃鍾之律,九寸加一寸為一尺。」夫度量權衡所 以取法於「黃鍾者,蓋貴其與天地之氣相應也。若加 一寸以為尺,則又何取於黃鍾?殊不知黃鍾之長,固 非人所能為。至於九其寸而為律,十其寸而為尺,則 人之所為也。《漢志》不知出此,乃欲加黃鍾一寸為尺, 謬矣。」何氏此論,發千載之祕,破萬世之惑,有功於律 學也大矣。此則唐、宋諸儒之所未發,惟我聖朝文明 之化所被,始有斯論,豈不偉哉!今復廣其說曰:「先儒 有言:一者,九之祖也,十百千萬之宗也。圓之而天,方 之而地,行之而四時。天所以覆物也,地所以載物也, 四時所以成物也。散之無外,卷之無內,體諸造化而 不可遺者乎!《雒書》,天道也,君道也,父道也,夫道也,交 道也,應變之道也;《河圖》,地道也」,臣道也,子道也,妻道 也,生道也,守常之道也。陽之情莫切於交,陰之情莫 急於生。交道右行相制,生道左旋相代,天地萬物生 民處世之道盡之矣。是故《河圖》非無奇也,而用則存 乎耦;《雒書》非無耦也,而用則存乎奇。耦者陰陽之對 待,奇者五行之迭運。對待者不能孤,迭運者不可窮。 天地之形,四時「之成,人物之生,萬化之凝,其妙矣乎! 天地之位也,四時之運也,陰陽感而五行播矣。五行, 陰陽也;陰陽,五行也。天地絪縕,萬物化醇;男女搆精, 萬物化生。無極之真,二五之精,妙合而凝,化化生生, 莫測其神,莫知其能,而可以一言盡之,黃鍾是也。」故 黃鍾之長,從黍八十一,分而為九寸,因而為律曆之 「元,其長橫黍十寸而為百分,因而為律曆之母」,皆取 法於《河圖》《雒書》,其義精矣。故何氏之說,雖與先儒異, 而實同也。
律義
周景王問律於伶州鳩,對曰:「律所以立均出度也。古 之神瞽,考中聲而量之以制,度律均鍾,百官軌儀。紀 之以三,平之以六,成於十二,天之道也。夫六,中之色 也,故名之曰黃鍾,所以宣養六氣九德也。由是第之。 二曰太蔟,所以金奏,贊陽出滯也。三曰姑洗,所以修 潔百物,考神納賓也。四曰蕤賓,所以安靖神人,獻酬」 交酢也。五曰《夷則》,所以詠歌九則,平民無貳也。六曰 《無射》,所以宣布哲人之令德,示民軌儀也。為之六間, 以揚沈伏而黜散越也。元間大呂,助宣物也。二間夾 鍾,出四隙之細也。三間中呂,宣中氣也。四間林鍾,和 展百事,俾莫不任肅純恪也。五間南呂,贊陽秀也。六 間應鍾,均利器用,俾應復也。律呂不「易,無姦物也。大 昭小鳴,和之道也。和平則久,久固則純,純明則終,終 復則樂,所以成政也,故先王貴之。」司馬遷《律書》曰:「七 正二十八舍律曆,天所以通五行八正之氣,天所以 成就萬物也。舍者,日月所舍。舍者,舒氣也。廣莫,風居 北方。廣莫者,言陽氣在下,陰莫,陽廣大也,故曰廣莫 東至於虛。」虛者,能實能虛。言陽氣冬則宛藏於虛日。 冬至則一陰下藏,一陽上舒,故曰「虛。」「東至於《須女》」,言 萬物變動其所,陰陽氣未相離,尚相如胥也,故曰「須 女。」十一月也,律中黃鍾。黃鍾者,陽氣踵黃泉而出也。 其於十二子為子。子者,滋也,滋者,言萬物滋於下也。 其於十母為壬癸。壬之為言任也,言陽氣任養萬物 於下也。癸之為言揆也,言萬物可揆度,故曰「癸。」東至 牽牛。牽牛者,言陽氣牽引萬物出之也。牛者,冒也,言 地雖凍,能冒而生也。牛者,耕植種萬物也。東至於建 星。建星者,建諸生也。十二月,律中大呂。大呂者,其於 十二子為丑。丑者,紐也,言陽氣在上,未降,萬物厄紐, 未敢出。條風居東北,主出萬物。條之,言條治萬物而 出之,故曰「條風。」「南至於箕。」箕者,言萬物根棋,故曰箕 正月也。律中太蔟。太蔟者,言萬物蔟生也,故曰太蔟。 其於十二子為寅,寅,言萬物始生螾然也,故曰「寅。」「南 至於尾」,言萬物始生如尾也。「南至於心」,言萬物始生 有華心也。「南至於房。」房者,言萬物門戶也,至於門則 出矣。明庶風居東方,明庶者,明眾物盡出也。二月也, 律中《夾鍾》。夾鍾者,言陰陽相夾廁也。其於十二子為 卯。卯之為言茂也,言萬物茂也。其於十母為《甲乙》。甲者,言萬物剖符甲而出也。乙者,言萬物生軋軋也。南 至於氐。氐者,言萬物皆至也。南至於亢。亢者,言萬物 亢見也。南至於角。角者,言萬物皆有枝格如角也。三 月也,律中姑洗。姑洗者,言萬物洗生。其於十二子為 辰。辰者,言萬物之蜄也。清明,風居東南維主風吹萬 物而西之軫軫者,言萬物益大而軫軫然。西至於翼。 翼者,言萬物皆有羽翼也。四月也,律中仲呂。仲呂者, 言萬物盡旅而西行也。其於十二子為巳。巳者,言陽 氣之已盡也。西至於七星。七星者,陽數成於七,故曰 「七星。」「西至於張。」張者,言萬物皆張也。西至於注。注者, 言萬物之始衰,陽氣下注,故曰注。五月也,律中蕤賓。 蕤賓者,言陰氣幼少,故曰蕤;痿。陽不用事,故曰賓。景 風居南方。景者,言陽氣道竟,故曰「景風。」其於十二子 為午。午者,陰陽交,故曰午。其於十母為丙丁。丙者,言 陽道著明,故曰丙;丁者,言萬物之丁壯也,故曰「丁。」「西 至於弧。」弧者,言萬物之吳落且就死也。「西至於狼。」狼 者,言萬物可度量,斷萬物,故曰狼。涼風居西南維主 地。地者,沈奪萬物氣也。六月也,律中《林鍾》。林鍾者,言 萬物就死,氣林林然。其於十二子為未。未者,言萬物 皆成,有滋味也。北至於罰。罰者,言萬物氣奪,可伐也。 北至於參。參言萬物可參也,故曰參,七月也。律中《夷 則》。夷則,言陰氣之賊萬物也。其於十二子為申。申者, 言陰用事,申賊萬物,故曰申。北至於濁。濁者,觸也,言 萬物皆觸死也,故曰「『濁。」北至於留。留者,言陽氣之稽 留也,故曰「留』,八月也,律中南呂。」南呂者,言陽氣之旅 入藏也。其於十二子為酉。酉者,萬物之老也,故曰酉。 《閶闔》,風居西方。閶者,倡也;闔者,藏也。言陽氣道萬物, 闔黃泉也。其於十母為庚辛。庚者,言陰氣庚萬物,故 曰庚;辛者,言萬物之辛生,故曰辛。北至於胃。胃者,言 陽氣就藏,皆胃胃也。北至於婁。婁者,呼萬物且內之 也。北至於奎。奎者,主毒螫殺萬物也,奎而藏之。九月 也,律中無射。無射者,陰氣盛用事,陽氣無餘也,故曰 「無射。」其於十二子為戌。戌者,言萬物盡滅,故曰戌不。 《周風》居西北,主殺生。東壁居不周風東,主辟生氣,而 東之至於營室。營室者,主營胎陽氣而產之,東至於 危。危,垝也,言陽氣之危垝,故曰危。十月也,律中應鍾。 應鍾者,陽氣之應,不用事也。其於十二子為亥。亥者, 該也,言陽氣藏於下,故該也。音始於宮,窮於角;數始 於一,終於十,成於三;氣始於冬至,周而復生。神生於 無形,成於有形,然後數形而成聲。故曰:「神使氣,氣就 形。」形理如類,有可類,或未形而未類,或同形而同類, 類而可班,類而可識。聖人知天地識之別,故從有以 至未有,以得細若氣,微若聲。然聖人因神而存之,雖 妙必效情,核其華道者明矣。非有聖心以乘聰明,孰 能存天地之神,而成形之情哉?神者,物受之而不能 知,及其去來,故聖人畏而欲存之。唯欲存之,神之亦 存。其欲存之者,故莫貴焉。故璿璣玉衡,以齊七政,即 天地二十八宿,十母十二子鍾律調。自上古建律運 曆造日度,可據而度也。合符節,通道德,即從斯之謂 也。蔡元定曰:「律者,陽氣之動,揚聲之始,必聲和氣應, 然後可以見天地之心。然非精於曆數,則氣節亦未 易正也。」是知律與曆蓋相須為用,不知律不可與言 曆,不知曆亦不可與言律。欲候氣以驗律,必測景以 正曆,此先後之序也。
律數
至治之世,天地之氣,合以生風,天地之風氣正十二 律,定十二律者,六律為陽,六呂為陰律以統氣類物。 一曰黃鍾,二曰太蔟,三曰姑洗,四曰蕤賓,五曰夷則, 六曰無射。呂以旅陽宣氣,一曰大呂,二曰夾鍾,三曰 仲呂,四曰林鍾,五曰南呂,六曰應鍾,有三統之義焉。 故黃鍾為天統,林鍾為地統,太蔟為人統。黃鍾者,陽 氣施種於黃泉,孳萌萬物,為六氣元也。變動不居,周 流六虛。始於子,在十一月。大呂:呂,旅也,言陰大旅助 黃鍾宣氣而芽物也。位於丑,在十二月。《太蔟》:蔟,奏也, 言陽氣大,奏地而達物也。位於寅,在正月。夾鍾:言陰 夾助太蔟宣四方之氣而出種物也。位於卯,在二月。 《姑洗》:洗,潔也,言陽氣洗物,辜潔之也。位於辰,在三月。 仲呂:言微陰始起未成,著於其中,旅助姑洗,宣氣齊 物也。位於巳,在四月。《蕤賓》:蕤,繼也;賓,導也,言陽始導 陰氣,使繼養物也。位於午,在五月。《林鍾》:林,君也,言陰 氣受任,助蕤賓君主種物,使長大楙盛也。位於未,在 六月。《夷則》:則,法也,言陽氣正法度,而使陰氣夷當傷 之物也。位於申,在七「月。《南呂》:南,任也,言陰氣旅助夷 則,任成萬物也。位於酉,在八月。《無射》」:射,厭也,言陽氣 究物,而使陰氣畢剝落之,終而復始,無厭已也。位於 戌,在九月。《應鍾》:言陰氣應無射,該藏萬物,而雜陽閡 種也。位於亥,在十月。三統者,天施地化,人事之紀也。 故陰陽之施化,萬物之終始,既類旅於律呂,又經歷 於日「辰,而變化之情可見矣。玉衡杓建,天之綱也;日 月初躔,星之紀也。綱紀之交,以原始造設,合樂用焉。 律呂唱和,以育生成化,歌奏用焉。指顧取象,然後陰陽萬物,靡不條鬯該成。故曰:『制禮上物,不過十二,天 之大數也』。」按律曆二術,皆生於黃鍾,古有是說。推原 是說之由,蓋謂天之大數不過十二,是故度律均鍾, 與夫百事軌儀,紀之以三,平之以六,而成於十二也。 所謂「紀之以三」者,若三十度為一辰,三十日為一月, 三百六十為一期,三十年為一世,三百年為一限之 類是也。所謂「平之以六」者,若六時為晝,六時為夜,六 月為盈,六月為縮。六律配五聲,合為六十調;六甲配 五子,合為六十日。六十年「赤道退天一度」之類是也。 所謂成於十二者,若黃鐘之生十二律,而循環無端, 以象天之十二方位,日之十二躔次,月之十二盈虧, 星辰之十二宮,斗杓之十二建,歲之十二月,日之十 二時,如是之類,皆與律呂之數相符,是故測景候氣 而與脗合。古之所謂曆法生於黃鐘,此之謂歟!
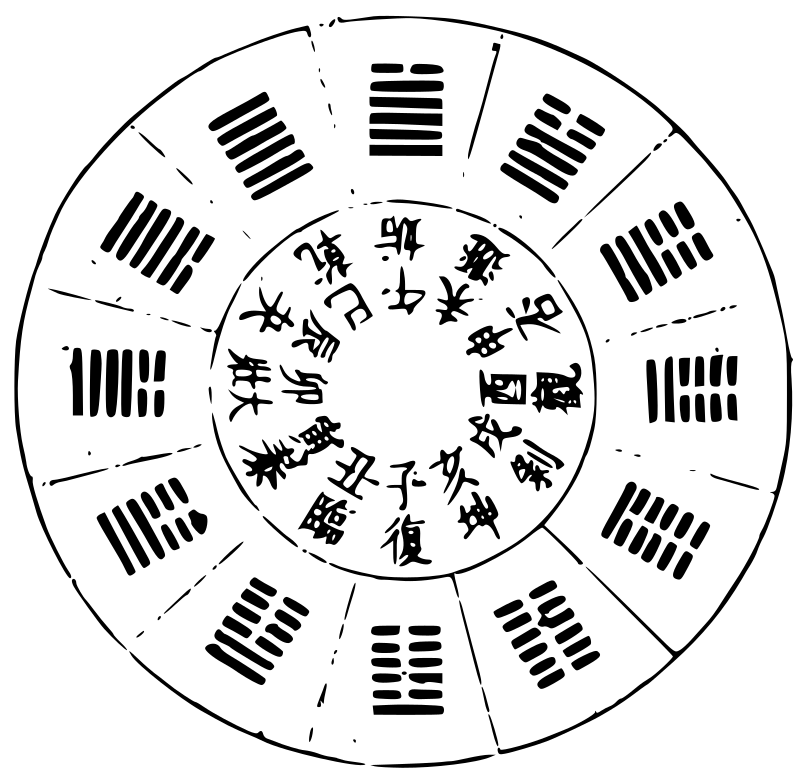
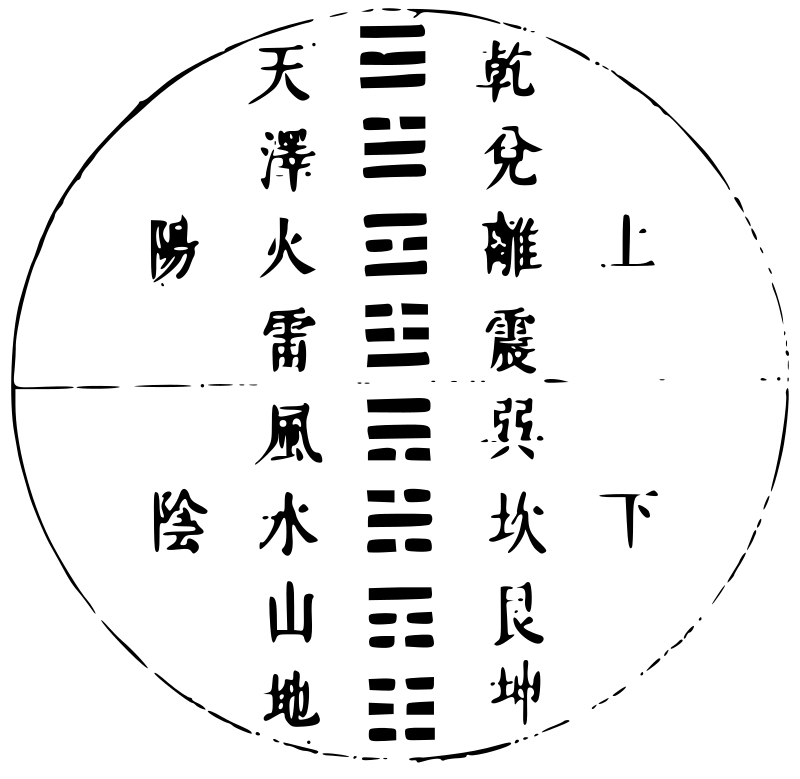
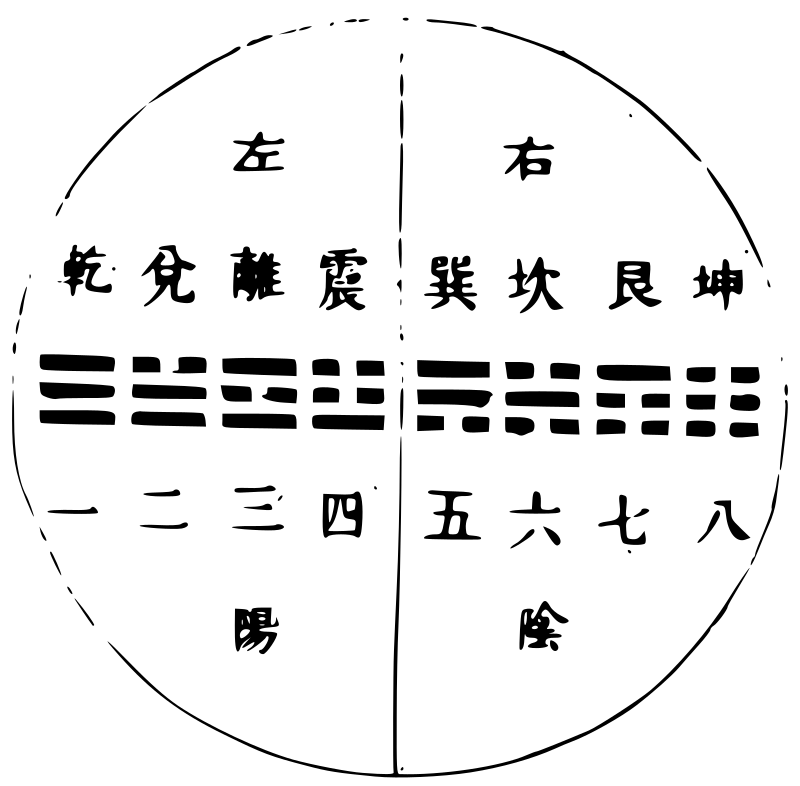
十二律呂以配卦象之圖
十二律呂以配卦象之圖
律象
十二律呂以配卦象。其法自《復》卦一陽生,屬子為冬 至;十一月中,《臨》卦二陽生,屬丑為大寒;十二月中,《泰》 卦三陽生,屬寅為雨水;正月中,「《大壯》四陽生,屬卯為 春分;二月中,《夬》卦五陽生,屬辰為穀雨;三月中,《乾》卦 六陽生,屬巳為小滿;四月中為純陽」之卦,陽極則陰 生。故《姤》卦一陰生,屬午為夏至;五月中,《遯》卦二陰生, 「屬未為大暑;六月中,《否》卦三陰生,屬申為處暑;七月 中;《觀》卦四陰生,屬酉為秋分;八月中。《剝》卦五陰生,屬 戌為霜降;九月中,《坤》卦六陰生,屬亥為小雪;十月中 為純陰之卦,陰極則陽生,又繼以十一月之復焉。」陰 陽消長,如環無端,不特見之卦畫之生如此,而卦氣 之運亦如此,自然與律之陰陽消長,相為配合。《大傳》 所謂「《易》與天地準,故能彌綸天地之道」,於此亦可見 其一端。故十二卦順四時之氣,配四方之位,實與伏 羲六十四卦圓圖之位次合。卦氣流行之接,卦畫對 待之妙,陰陽盛衰消長,相為倚伏之機,備於此十二 月卦中矣。謹按十二律配卦象,其原出於《易緯》,而諸 家所主不一,邵雍已前未聞有圖。雍所傳《先天圖》,蓋 出於陳希夷。朱熹謂此圖希夷已前原有,但祕而不 傳,惟方士輩相傳授耳。《參同契》所言是也。今考《參同 契》之文,於《復》則曰「黃鍾建子」,《臨》則曰「丑之大呂」,《泰》則 曰「輻輳於寅」,輳指太蔟言也;《大壯》則曰「俠列卯門」,俠 指夾鍾言也。他卦放此。結之曰:「終坤始復,如循連環。」 此一節文義與《六十四卦圓圖》全合,惟與《方圖》不合, 疑舊圖世遠,或傳寫之誤歟?何瑭嘗作一圖,其卦次 第自上而下,曰:「以伏羲橫圖豎起觀之,則造化在目 中矣。夫坤者地也,故居最下。地之上有山焉,山之上 有水焉,水之上有風焉,風之上有雷焉,雷之上有火 焉,日電之屬是也。火之上有澤焉,霄漢之」類是也。澤 之上有天而已,故乾居最上焉,皆自然之次序,非有 所穿鑿也。《瑭》又曰:「火陽也,雖附於天而未嘗不行於 地;水陰也,雖附於地而未嘗不行於天。水火者,天地 之二用也,雨雪霜露,皆澤之類也。」此圖舊所未有,實 自瑭始。今推究之,然則八卦橫圖一數,當從左起,左 陽右陰故也。或疑非逆行乎?曰:非也。自左而右是順, 從右而左為逆。凡四時五行干支方位,皆由左而後 右,匪惟卦象爾耳。至於書數亦然。故蒼頡造書,隸首 作數,下筆布算,先自左方。後世巧者,莫能易之。此造 化自然,非人所為也。故知橫圖從右起者誤矣。《從圖》 《橫圖》《方圖》,皆係新作,與舊不同,今列於後。
右按:上文以橫圖為內卦,配從圖為外卦,經緯錯綜, 成卦六十有四,則西邊之下卦,北邊之上卦,皆坤,西 與北,陰方也。有《坤》而無乾,古云「天傾西北」,此也。東邊 之下卦,南邊之上卦,皆乾,東與南,陽方也。有乾而無 《坤》,古云「地不滿東南」,此也。乾坤交於寅為《泰》,塞於申 為《否》,古云「寅申為陰陽祖」,此也。子午卯酉,四正之位 「也,《復》《姤》《大》《壯》《觀》四卦居之,按四仲月以應分至焉。寅、 申己、亥,四隅之位也,《泰》《否》《乾》《坤》四卦居之,按四孟月 以應啟閉焉。辰、戌丑、未,中央土之位也,《夬》《剝》《臨》《遯》四 卦居之,按四季月以應寄旺焉。」十二月卦次序,適與 十二支方位相合,亦自然之理,而先儒所未發也。然 自漢以來,曆家皆主六日七分之術以推卦氣,其說 不經。至於觀陰陽之變,則錯亂而不明。今依何氏改 定,自與先天圖合,詳見下卷《爻象》篇。
